PAWE Version 2.1
Help File, May 2014
Written by Derek Gordon
1.
Overview and Purpose
a.
The name of
this program is PAWE, which stands for Power
of Association With Errors. Over the
years, there have been numerous publications documenting the presence of genotype
misclassification errors and methods to detect and address these errors in
statistical analyses. See Pompanon et al. (2005), Gordon and Finch (2005), and Miller et al. (2008) for reviews.
b.
Among
genotype misclassification errors, there are two types: (i) differential, in
which error rates are different in cases and controls; and (ii)
non-differential, in which error rates are the same. The effect of differential
misclassification errors is an increase in the false positive rate, i.e., when
the null hypothesis is true (similar to population stratification). The effect
of non-differential misclassification is a decrease in statistical power to
detect association. The PAWE webtool considers only non-differential genotype
misclassification.
c.
The purposes
of the PAWE program are two-fold: (i) to compute power and sample size
calculations for genetic case-control association studies in the presence of genotype
misclassification errors; and (ii) to determine quantitatively how much, in
terms of decrease in asymptotic power for a fixed sample size, or increase in
sample size to maintain constant asymptotic power, errors cost the researcher
performing genetic association studies with cases and controls. Thus, results
from the PAWE program will be either asymptotic power or sample size values.
d.
This file is
designed to explain to you the different values entered into the PAWE program,
so that a meaningful answer is obtained. This program is designed to perform
asymptotic power and sample size calculations for genetic case-control studies
with a di-allelic locus (for example, a SNP) in the presence of
misclassification. The test statistics considered are the linear trend test and
the chi-square statistic for genotypic association. In what follows, it will be
assumed that there is a di-allelic trait locus for a discrete trait with two
alleles: a wild-type allele or low risk allele, denoted by +, and a trait or
high-risk allele, denoted by 
. Also, it will be assumed that
there is a marker locus with two alleles, denoted by 1 and 2.
2.
Parameter Settings
a.
Asymptotic
Power or Sample Size
i.
The
researcher who has a fixed sample size and wants to know the value of
asymptotic power for his/her study in the presence of errors should choose the
option "Power for a fixed sample size".
1.
Number
of cases
In this box, you specify the number of case individuals you have.
These individuals are assumed to be both phenotyped and genotyped. The number
typed in this box must be a positive integer.
2.
Number
of controls
In this box, you specify the number of control individuals you
have. These individuals are assumed to be both phenotyped and genotyped. The number typed in this box must be a
positive integer.
ii.
The
researcher who is planning a study, and who wants to know what sample size is
necessary, in the presence of errors, to achieve a given asymptotic power level
should choose "Sample size for fixed power".
1.
Asymptotic
Power level
In this box, you specify the asymptotic power you would like for
your study. This number must be greater than 0 and less than or equal to 1. It
is usually a number closer to 1.
2.
Ratio
of Controls to Cases
In this box, you specify the ratio of the number of controls to
the number of cases that you expect to have for your study. The number entered
here must be a positive real number. The most common number used is 1 (equal
number of cases and controls).
b.
Significance
level
Here, you specify the significance level of the test. This value
is the probability of falsely rejecting a true null hypothesis. This number
must be positive and less than 1. Typically, it is chosen to be less than or
equal to 0.05.
c.
Genotype
Frequency Generation
i.
Genetic
model free method
You choose this option if you do not know or do not want to
specify the genetic model parameters such as disease prevalence, disease allele
frequency, genotype relative risks, or proportion of linkage disequilibrium 
for your study. When choosing the genetic
model free method, you specify the frequency distribution of genotypes 11, 12,
and 22 for cases and controls. You may specify or not specify Hardy Weinberg Equilibrium
(HWE) for the case and control populations.
1.
Hardy
Weinberg Equilibrium specified
If you specify HWE, then the genotype frequency distribution is a function
of two parameters, 
(1 allele frequency in cases)
and 
(1 allele frequency in controls). These parameters must be real,
positive numbers less than 1. The genotype frequencies of 11, 12, and 22 in
cases (respectively, controls) are: 
, 
and 
, 
, respectively.
2.
No
Specification of Hardy Weinberg Equilibrium
If you do not specify HWE, then the genotype frequencies are a function
of four parameters: 
(11 genotype frequency in cases); 
(22 genotype frequency in cases); 
(11 genotype frequency in controls); 
(22 genotype frequency in controls). Note that the parameters are
all real, positive numbers subject to the constraints:
;
.
Note also that the heterozygote genotype frequencies in cases and
controls are given by the formulas:
;
.
ii.
Genetic
model based method
You choose this option if you have estimates for the following six
parameters: the disease prevalence 
; the genotype relative risks 
and 
(Schaid
and Sommer, 1993); the disease allele frequency 
; the marker 1-allele frequency ; and a measure of linkage disequilibrium
between alleles d and 1 . With the exception of the
genotype relative risks, all parameters must be positive real numbers that are
less than one. The genotype relative risks are defined as:
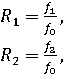
where 
.
The values 
, are commonly referred to as
the penetrance values.
Some common disease modes of inheritance are determined by
constraints on the genotype relative risk. For example:
In PAWE, you enter the value and the mode of inheritance, and the
program computes the value. Note that, if no constraints are placed on and (we use the term “unconstrained”), then they
can be any positive numbers greater than one. Finally, we mention that 
= 1 means complete disequilibrium,
the scenario with the highest power, and = 0 means no disequilibrium, the
null scenario (no power).
d.
Linear Trend
Test Weights
Here, you specify the weights of the trend test statistic,
corresponding to the genotypes 11, 12, and 22. The weights reflect an ordering
of the genotypes. For example, in our work, the risk allele at a SNP locus is
the 1 allele. If we have a dominant mode of inheritance, then we expect that
the 22 genotype does not increase risk, while the 11 and 12 genotypes do. We
may choose the weights (1, 1, 0) for the 11, 12, and 22 genotypes respectively.
Similarly, suppose that the trait acted in a recessive manner. Then we would
choose the weights (1,0,0) for the 11, 12, and 22 genotypes respectively. The most
commonly used weights for unknown modes of inheritance are (2,1, 0). See Slager
and Schaid (2001) for more information.
Very important note: If you choose weights that do
not reflect the true risk genotypes, your sample sizes for a fixed power will
increase dramatically. Similarly, your power for a fixed sample size will drop
dramatically. For example, in the first example above, if you choose the
weights (0,1,1) instead of (1,1,0), you will either lose power or increase
sample size (two undesirable effects). When in doubt, we recommend that you use
the (2,1,0) weights.
e.
Genotype
Error Model
For this option, you have the choice of selecting one of three
error models that you think best explains your data. The choices are:
i.
Gordon
Heath Liu Ott (GHLO) error model (Gordon
et al., 2001)
The parameter settings for this
error model are:
;
.
Both entries must be positive real numbers less than 1.0. Note
that in this error model, loci that are in HWE before errors are still in HWE
after introduction of errors.
ii.
Douglas Skol Boehnke error model (Douglas et al., 2002)
The parameter settings for this error model are:
;
.
Both entries must be positive real numbers less than 1.0. In this
error model, it is not possible for one homozygote (e.g., 11) to be
misclassified as another (e.g., 22). Also, for the 
parameter, we specify that the 12 genotype
(heterozygote) has an equal probability (0.5) of being incorrectly coded as 11
or 22 (homozygotes). See (Gordon
et al., 2001) for more details.
iii.
Mote
and Anderson error model
(Mote
and Anderson, 1965)
The parameter settings for this model are:
= Pr(12 genotype observed | 11
true);
= Pr(22 genotype observed | 11
true);
= Pr(11 genotype observed | 12 true);
= Pr(22 genotype observed | 12
true);
= Pr(11 genotype observed | 22
true);
= Pr(12 genotype observed | 22
true).
The MA model is the most general error model possible in that it
can describe all other error models. As noted above, the MA model is described
by 6 parameters. The GHLO and MA error
models allow for errors in which one homozygote is incorrectly miscoded as another
homozygote. The following constraints are needed for the MA error model:
3.
Program Output
The PAWE program reports most of
the input parameters that the user enters, as well as the following items:
a.
Non-centrality
parameter
i.
For a given
test of association (linear trend or genotypic), this parameter completely
determines either the asymptotic power or sample size calculations. To see how
the asymptotic power calculations are performed, please see Ahn et al. (2007) and Gordon et al. (2002). The non-centrality parameters
for both errorless data and data with errors are presented.
ii.
Asymptotic
power for fixed sample size: power loss
Based on the value of the non-centrality parameter for either the
linear trend or genotypic test of association, the asymptotic power of the test
is reported for both errorless data and data assuming the particular error
model. Also reported is the percent loss in power due to errors in the data.
iii.
Sample
size increase for fixed asymptotic power
Based on the value of the non-centrality parameter for either the
linear trend or genotypic test of association, the minimum sample of cases and
controls is reported for both errorless data and data given the particular
error model. Also reported is the percent increase in sample size needed to
maintain constant power when errors are present.
b.
Genotype
frequencies for errorless data
Based on the parameters entered for genotype frequency generation (Section
2.c), the genotype frequencies in cases and controls are computed for errorless
data.
c.
Matrix of
Penetrances
The entries of this matrix are the conditional probabilities
Pr(observed genotype i | true
genotype j) where i and j are in the set of the genotypes 11, 12, or 22. These conditional probabilities, also
called penetrances, are used in calculating the genotype frequencies in the
presence of errors (see Section 3.d).
d.
Genotype frequencies
for error data
Using the genotype frequencies in cases and controls for errorless
data (Section 3.b), and the matrix of penetrances (Section 3.c), genotype frequencies
in cases and controls are computed for error data. These values are used to
compute the non-centrality parameters for error data (Section 3.a). For more details
on how this computation is performed, please see Gordon et al (2002) and Ahn et al. (2007).
Please
cite the references below in bold when using results from the PAWE webtool.
References
Ahn, K., Haynes, C., Kim, W., Fleur, R.S., Gordon, D., and Finch, S.J.
(2007). The effects of SNP genotyping errors on the power of the
Cochran-Armitage linear trend test for case/control association studies. Ann
Hum Genet 71, 249-261.
Douglas, J.A., Skol, A.D., and Boehnke, M. (2002). Probability of
detection of genotyping errors and mutations as inheritance inconsistencies in
nuclear-family data. Am J Hum Genet 70,
487-495.
Gordon, D., and Finch, S.J. (2005). Factors affecting statistical power in
the detection of genetic association. J Clin Invest 115, 1408-1418.
Gordon, D.,
Finch, S.J., Nothnagel, M., and Ott, J. (2002). Power and sample size
calculations for case-control genetic association tests when errors are
present: application to single nucleotide polymorphisms. Hum Hered 54, 22-33.
Gordon, D., Heath, S.C., Liu, X., and Ott, J. (2001). A
transmission/disequilibrium test that allows for genotyping errors in the
analysis of single-nucleotide polymorphism data. Am J Hum Genet 69, 371-380.
Miller, M.B., Schwander, K., and Rao, D.C. (2008). Genotyping errors and
their impact on genetic analysis. Adv Genet
60, 141-152.
Mote, V.L., and Anderson, R.L. (1965). An Investigation of the Effect of
Misclassification on the Properties of Chi-2-Tests in the Analysis of
Categorical Data. Biometrika 52,
95-109.
Pompanon, F., Bonin, A., Bellemain, E., and Taberlet, P. (2005).
Genotyping errors: causes, consequences and solutions. Nat Rev Genet 6, 847-859.
Schaid, D.J., and Sommer, S.S. (1993). Genotype relative risks: methods
for design and analysis of candidate-gene association studies. Am J Hum Genet 53, 1114-1126.
Slager, S.L., and Schaid, D.J. (2001). Case-control studies of genetic markers:
power and sample size approximations for Armitage's test for trend. Hum Hered 52, 149-153.